A Guide to Rate Laws and Reaction Rates
A GUIDE TO RATE LAWs AND REACTION RATES
Combination: A + B → C, where C is a new compound composed of some ratio of elements A and B
2Na + Cl2 → 2NaCl
Displacement: A + BC → AB + C, where C is displaced from A
Double replacement: AB + CD → AC + BD
Pb(NO3)2 + Na2SO4 → PbSO4 + 2NaNO3
to name only a few. While there are billions of possible chemical, enzymatic, or complexation reactions, each proceeds with a particular reaction rate, the study of which is known as chemical kinetics. The rate of reaction is dependent on a variety of factors, such as temperature, pH, concentration, solid surface area, pressure, etc. Measuring the rate of reaction allows for optimization of all these parameters and may provide insight into reaction intermediates and overall mechanism.
The concentration(s) of the reagent(s) involved in a chemical reaction is easily varied and is related to the rate of reaction through a type of equation known as a rate law.
For a simple combination reaction as described above, the rate law is
rate = k[A]m[B]n
where k is the rate constant of the reaction, [A] and [B] are the concentrations of reagents A and B (usually in M, moles per liter), and the exponents m and n are the orders of reaction of A and B (more on that later). Note that only the concentrations of the reactants are present in the rate law, no products.
One of the more practical applications of measuring a reaction’s rate constant is derivation of the associated reaction half-life. The half-life of a reaction is the time needed for the concentration of a reactant to decrease to one-half of its initial value and is a useful parameter in estimating the length of time for a reaction to reach completion (i.e., two hours, two days, or two weeks).
Types of Reaction Orders and their Rate Laws
So, what is a reaction order? In simple terms, the order of each particular reactant indicates how varying its concentration affects the overall reaction rate. For example, if a reaction is “first order in A,” doubling the concentration of A will double the reaction rate. If a reaction is “second order in B,” doubling the concentration of B will quadruple the reaction rate. Reactants with negative orders inversely impact the rate of reaction when their concentrations are increased, and those reactants that are zero-order have no effect on the reaction rate at all. Determining the overall reaction order is simple – it is simply the sum of the orders of each individual reactant.
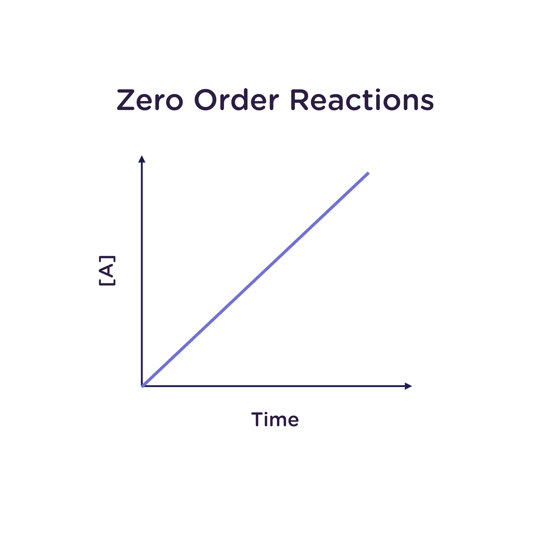
Zero Order Reactions
For a reaction which is in zero order, the reaction rate is independent of any change in the concentration of any of the reactants. This is particularly common in the case of enzymatic reactions, where the reactant is present in much higher concentration than the enzyme performing the transformation.
For a reaction that is zero order in A:
Rate law: -d[A]/dt = k
Integrated rate law: [A] = [A]0 - kt
Half-life: t1/2 = [A]0/2k
For a reaction that is zero order in A, a plot of the concentration of A ([A]) vs time gives a straight line with a slope equal to the rate constant k, which has units of M/s (“molar per second”).
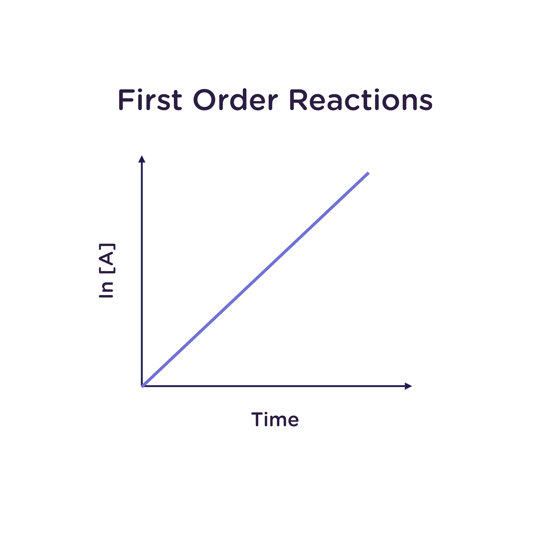
First Order Reactions
In a first-order reaction, the reaction rate depends on the concentration of only one species. This may be the case in an unimolecular reaction (a reaction with only one reactant) or in a reaction with more than one reactant in which all other reactants are zero order.
A reaction may be dubbed pseudo-first order if all other reactants are present far in excess of one reactant, such that changing the concentration of these excess reactants has no effect on the reaction rate. A good example of this is the hydrolysis of sucrose, where the water
performing the hydrolysis is far in excess of the sucrose dissolved in solution. It is of note that the half-life of a first-order reaction is independent of concentration.
For a reaction that is first order in A:
Rate law: -d[A]/dt = k[A]
Integrated rate law: [A] = [A]0 e(-kt)
Half-life: t1/2 = ln2/k
A reaction that is first order in A gives a straight line with slope k when the natural logarithm of the concentration of A (ln [A]) is plotted as a function of time. The units of the rate constant k are thus 1/s (“per second”).
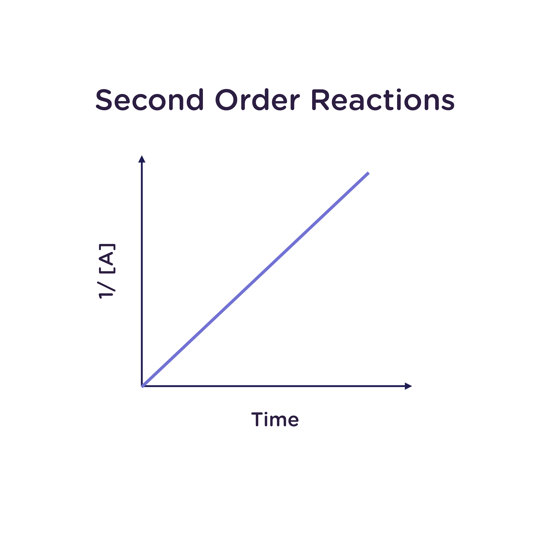
Second Order Reactions
A reaction is second order overall when it is second order in one reagent, zero order in all others, or first order for two reagents (1 + 1 = 2). For example, the combination reaction A + B → C would be second-order overall if first-order in both A and B.
For a reaction that is second order in A (not to be confused with first order in A, first order in B, and second order overall):
Rate law: -d[A]/dt = k[A]2
Integrated rate law: 1/([A]) = 1/[A]0 + kt
Half-life: t1/2 = 1/(k[A]0)
A plot of inverse concentration of A (1/[A]) as a function of time gives a straight line with slope k for a reaction that is second order in A. The units of k are 1/M·s (“per molar per second”).
Reactions with overall orders greater than two are possible but are very rare.
So, how do I determine the order of my reaction?
Determining the order of each reactant requires systematically varying its concentration and determining its effect on the overall reaction rate. As stated previously, if doubling the concentration of A increases the rate of reaction by a factor of two, the reaction is first order in A. If doubling the concentration of B quadruples the rate of reaction, the reaction is second order in B. Thus, determining the overall order of reaction relies upon determining the order of each individual reactant, which requires a reliable method of determining the reaction rate.
How do I measure the rate constant of my reaction?
The rate constant of a reaction can be measured using any method that can distinguish between the reaction product and its starting reagent(s). Changes in mass, NMR chemical shift, color (UV absorption band), fluorescence emission maximum or quantum yield, and circular dichroism signal are all commonly used markers to monitor the transformation of reactant(s) to product(s). Aliquots of the reaction mixture may be removed and analyzed using any of the previously listed methods, or for more quickly occurring reactions, the reagents may be mixed immediately prior to placing the sample within the instrument.
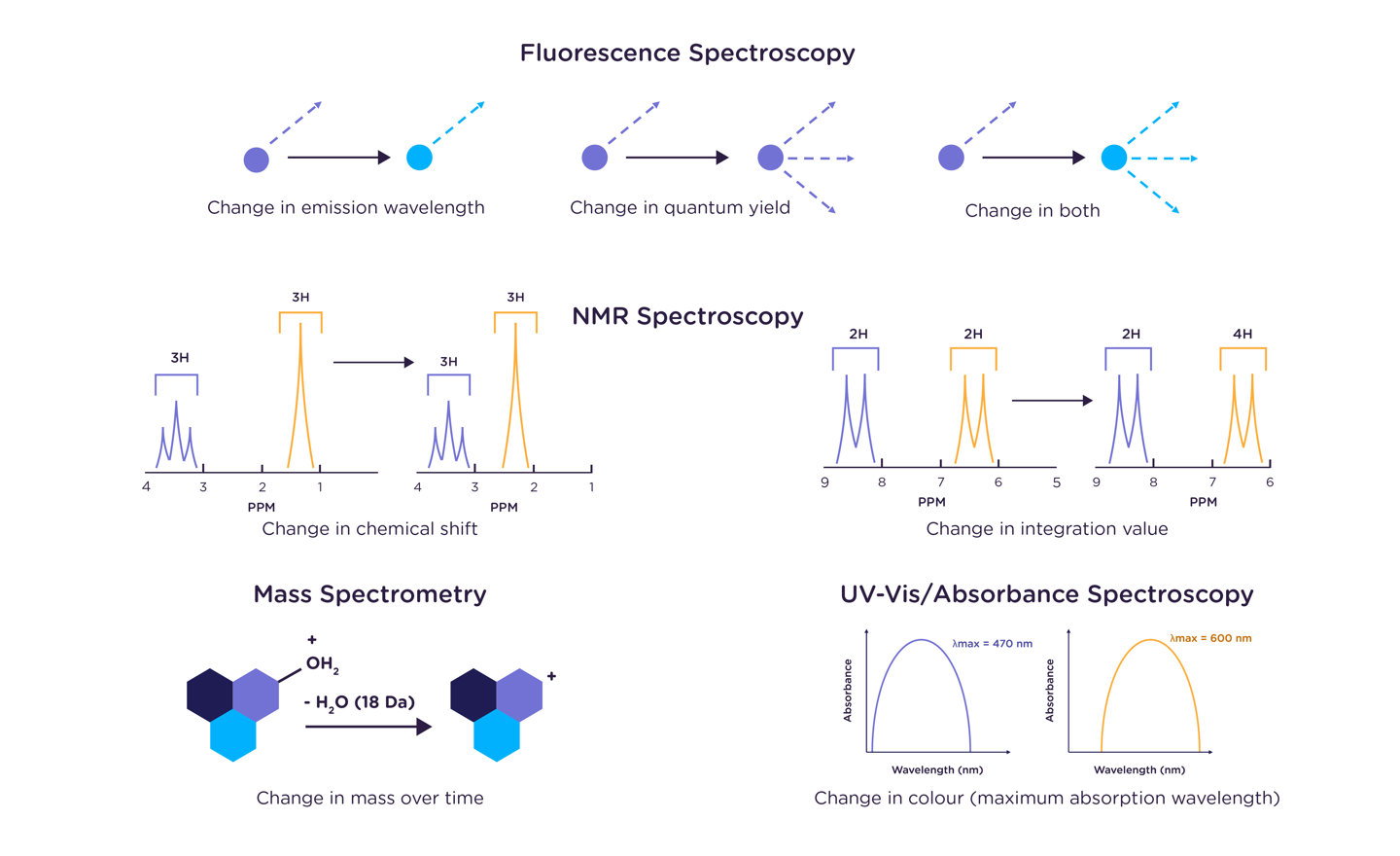
What if my reaction is too fast to measure by hand?
Stopped flow instrumentation is designed for when the rate of your reaction is simply too high to allow for standard (human) mixing. In the typical absorption- or fluorescence-based experiment, two (or more, in the case of sequential mixing) reagents are mixed together in a standard cuvette, which is then placed inside the spectrometer. Only once the “measure” button is pressed in the instrument software is any kinetic data collected.
For slower reactions, those on the timescale of minutes, hours, or even days, not much information is lost in the time taken to mix reagents together before collecting data. But what happens if the reaction you’re monitoring takes only seconds – or even milliseconds? Regardless of how quickly you can pipette, there’s no chance of collecting enough data points manually.
Stopped flow removes the human element from reagent mixing. Shown below is a schematic illustration of Applied Photophysics’ SX20 stopped-flow instrument. Rather than pipetting both reagents into a cuvette, the reagents are contained in two drive syringes, which are dispensed into a mixing line by the upward movement of the drive ram. The reagents are in contact for only a very short period of time prior to reaching the observation cell.
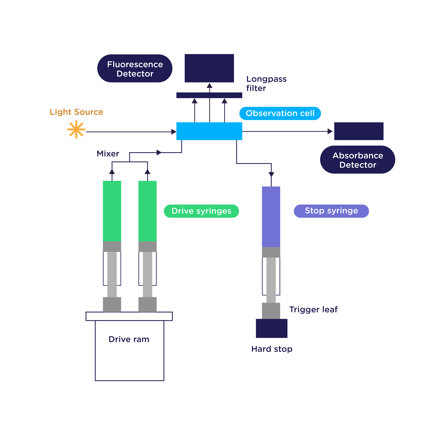
The new reagents are then mixed into the observation cell, pushing out any old reagents into the stop (waste) syringe. The stop syringe piston then pushes the trigger leaf against a hard stop, which "stops" the flow and begins data collection. The observation cell is irradiated with a particular wavelength of light, and PMT detectors are mounted at 180° (for absorbance) and 90° (for fluorescence), allowing monitoring of either signal as a function of time.
However, the reagents are still in contact prior to data collection, as the mixing takes place prior to reaching the observation cell!
Yes, that's true. The time the reagents are in contact prior to kinetic data being measured is called the instrument's dead time. Think of it as analogous to the time it would take you to pipette both reagents into a cuvette, place the cuvette into the instrument, and press measure, and it becomes clear that the stopped-flow dead time is much shorter!
The Applied Photophysics SX20 is specifically designed to minimize instrument dead time, such that you can start collecting useful data sooner. The standard 20 µL observation cell has a dead time of 1.1 ms, and for even faster reactions, a rapid mixing cell with a volume of 5 µL and a dead time of 0.5 ms is available.

Related:
